LSTM time series example¶
This tutorial shows how to use an LSTM model with multivariate data, and generate predictions from it. For demonstration purposes, we used an open source pollution data. The tutorial is an illustration of how to use LSTM models with MXNet-R. We are forecasting the air pollution with data recorded at the US embassy in Beijing, China for five years.
Dataset Attribution: “PM2.5 data of US Embassy in Beijing” We want to predict pollution levels(PM2.5 concentration) in the city given the above dataset.
Dataset description:
No: row number
year: year of data in this row
month: month of data in this row
day: day of data in this row
hour: hour of data in this row
pm2.5: PM2.5 concentration
DEWP: Dew Point
TEMP: Temperature
PRES: Pressure
cbwd: Combined wind direction
Iws: Cumulated wind speed
Is: Cumulated hours of snow
Ir: Cumulated hours of rain
We use past PM2.5 concentration, dew point, temperature, pressure, wind speed, snow and rain to predict PM2.5 concentration levels.
Load and pre-process the data¶
The first step is to load in the data and preprocess it. It is assumed that the data has been downloaded in a .csv file: data.csv from the pollution dataset
## Loading required packages
library("readr")
library("dplyr")
library("mxnet")
library("abind")
## Preprocessing steps
Data <- read.csv(file = "/Users/khedia/Downloads/data.csv",
header = TRUE,
sep = ",")
## Extracting specific features from the dataset as variables for time series We extract
## pollution, temperature, pressue, windspeed, snowfall and rainfall information from dataset
df <- data.frame(Data$pm2.5,
Data$DEWP,
Data$TEMP,
Data$PRES,
Data$Iws,
Data$Is,
Data$Ir)
df[is.na(df)] <- 0
## Now we normalise each of the feature set to a range(0,1)
df <- matrix(as.matrix(df),
ncol = ncol(df),
dimnames = NULL)
rangenorm <- function(x) {
(x - min(x))/(max(x) - min(x))
}
df <- apply(df, 2, rangenorm)
df <- t(df)
For using multidimesional data with MXNet-R, we need to convert training data to the form (n_dim x seq_len x num_samples). For one-to-one RNN flavours labels should be of the form (seq_len x num_samples) while for many-to-one flavour, the labels should be of the form (1 x num_samples). Please note that MXNet-R currently supports only these two flavours of RNN. We have used n_dim = 7, seq_len = 100, and num_samples = 430 because the dataset has 430 samples, each the length of 100 timestamps, we have seven time series as input features so each input has dimesnion of seven at each time step.
n_dim <- 7
seq_len <- 100
num_samples <- 430
## extract only required data from dataset
trX <- df[1:n_dim, 25:(24 + (seq_len * num_samples))]
## the label data(next PM2.5 concentration) should be one time step
## ahead of the current PM2.5 concentration
trY <- df[1, 26:(25 + (seq_len * num_samples))]
## reshape the matrices in the format acceptable by MXNetR RNNs
trainX <- trX
dim(trainX) <- c(n_dim, seq_len, num_samples)
trainY <- trY
dim(trainY) <- c(seq_len, num_samples)
Defining and training the network¶
batch.size <- 32
# take first 300 samples for training - remaining 100 for evaluation
train_ids <- 1:300
eval_ids <- 301:400
## The number of samples used for training and evaluation is arbitrary. I have kept aside few
## samples for testing purposes create dataiterators
train.data <- mx.io.arrayiter(data = trainX[, , train_ids, drop = F],
label = trainY[, train_ids],
batch.size = batch.size, shuffle = TRUE)
eval.data <- mx.io.arrayiter(data = trainX[, , eval_ids, drop = F],
label = trainY[, eval_ids],
batch.size = batch.size, shuffle = FALSE)
## Create the symbol for RNN
symbol <- rnn.graph(num_rnn_layer = 1,
num_hidden = 5,
input_size = NULL,
num_embed = NULL,
num_decode = 1,
masking = F,
loss_output = "linear",
dropout = 0.2,
ignore_label = -1,
cell_type = "lstm",
output_last_state = T,
config = "one-to-one")
mx.metric.mse.seq <- mx.metric.custom("MSE", function(label, pred) {
label = mx.nd.reshape(label, shape = -1)
pred = mx.nd.reshape(pred, shape = -1)
res <- mx.nd.mean(mx.nd.square(label - pred))
return(as.array(res))
})
ctx <- mx.cpu()
initializer <- mx.init.Xavier(rnd_type = "gaussian",
factor_type = "avg",
magnitude = 3)
optimizer <- mx.opt.create("adadelta",
rho = 0.9,
eps = 1e-05,
wd = 1e-06,
clip_gradient = 1,
rescale.grad = 1/batch.size)
logger <- mx.metric.logger()
epoch.end.callback <- mx.callback.log.train.metric(period = 10,
logger = logger)
## train the network
system.time(model <- mx.model.buckets(symbol = symbol,
train.data = train.data,
eval.data = eval.data,
num.round = 100,
ctx = ctx,
verbose = TRUE,
metric = mx.metric.mse.seq,
initializer = initializer,
optimizer = optimizer,
batch.end.callback = NULL,
epoch.end.callback = epoch.end.callback))
Output:
Start training with 1 devices
[1] Train-MSE=0.197570244409144
[1] Validation-MSE=0.0153861071448773
[2] Train-MSE=0.0152517843060195
[2] Validation-MSE=0.0128299412317574
[3] Train-MSE=0.0124418652616441
[3] Validation-MSE=0.010827143676579
[4] Train-MSE=0.0105128229130059
[4] Validation-MSE=0.00940261723008007
[5] Train-MSE=0.00914482437074184
[5] Validation-MSE=0.00830172537826002
[6] Train-MSE=0.00813581114634871
[6] Validation-MSE=0.00747016374953091
[7] Train-MSE=0.00735094994306564
[7] Validation-MSE=0.00679832429159433
[8] Train-MSE=0.00672049634158611
[8] Validation-MSE=0.00623159145470709
[9] Train-MSE=0.00620287149213254
[9] Validation-MSE=0.00577476259786636
[10] Train-MSE=0.00577280316501856
[10] Validation-MSE=0.00539038667920977
..........
..........
[91] Train-MSE=0.00177705133100972
[91] Validation-MSE=0.00154715491225943
[92] Train-MSE=0.00177639147732407
[92] Validation-MSE=0.00154592350008897
[93] Train-MSE=0.00177577760769054
[93] Validation-MSE=0.00154474508599378
[94] Train-MSE=0.0017752077546902
[94] Validation-MSE=0.0015436161775142
[95] Train-MSE=0.00177468206966296
[95] Validation-MSE=0.00154253660002723
[96] Train-MSE=0.00177419915562496
[96] Validation-MSE=0.00154150440357625
[97] Train-MSE=0.0017737578949891
[97] Validation-MSE=0.00154051734716631
[98] Train-MSE=0.00177335749613121
[98] Validation-MSE=0.00153957353904843
[99] Train-MSE=0.00177299699280411
[99] Validation-MSE=0.00153867155313492
[100] Train-MSE=0.00177267640829086
[100] Validation-MSE=0.00153781197150238
user system elapsed
21.937 1.914 13.402
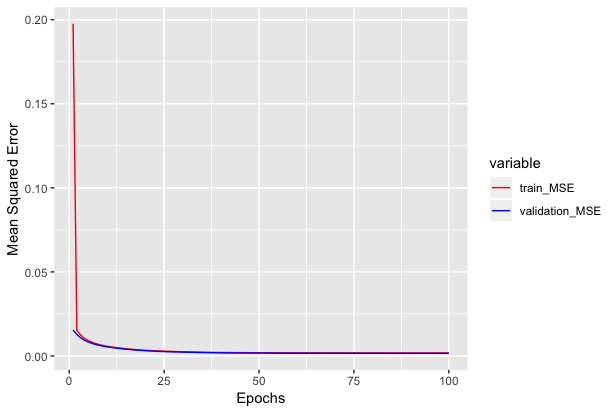
We can see how mean squared error varies with epochs below.
Inference on the network¶
Now we have trained the network. Let’s use it for inference.
## We extract the state symbols for RNN
internals <- model$symbol$get.internals()
sym_state <- internals$get.output(which(internals$outputs %in% "RNN_state"))
sym_state_cell <- internals$get.output(which(internals$outputs %in% "RNN_state_cell"))
sym_output <- internals$get.output(which(internals$outputs %in% "loss_output"))
symbol <- mx.symbol.Group(sym_output, sym_state, sym_state_cell)
## We will predict 100 timestamps for 401st sample (first sample from the test samples)
pred_length <- 100
predicted <- numeric()
## We pass the 400th sample through the network to get the weights and use it for predicting next
## 100 time stamps.
data <- mx.nd.array(trainX[, , 400, drop = F])
label <- mx.nd.array(trainY[, 400, drop = F])
## We create dataiterators for the input, please note that the label is required to create
## iterator and will not be used in the inference. You can use dummy values too in the label.
infer.data <- mx.io.arrayiter(data = data,
label = label,
batch.size = 1,
shuffle = FALSE)
infer <- mx.infer.rnn.one(infer.data = infer.data,
symbol = symbol,
arg.params = model$arg.params,
aux.params = model$aux.params,
input.params = NULL,
ctx = ctx)
## Once we get the weights for the above time series, we try to predict the next 100 steps for
## this time series, which is technically our 401st time series.
actual <- trainY[, 401]
## Now we iterate one by one to generate each of the next timestamp pollution values
for (i in 1:pred_length) {
data <- mx.nd.array(trainX[, i, 401, drop = F])
label <- mx.nd.array(trainY[i, 401, drop = F])
infer.data <- mx.io.arrayiter(data = data,
label = label,
batch.size = 1,
shuffle = FALSE)
## note that we use rnn state values from previous iterations here
infer <- mx.infer.rnn.one(infer.data = infer.data,
symbol = symbol,
ctx = ctx,
arg.params = model$arg.params,
aux.params = model$aux.params,
input.params = list(rnn.state = infer[[2]],
rnn.state.cell = infer[[3]]))
pred <- infer[[1]]
predicted <- c(predicted, as.numeric(as.array(pred)))
}
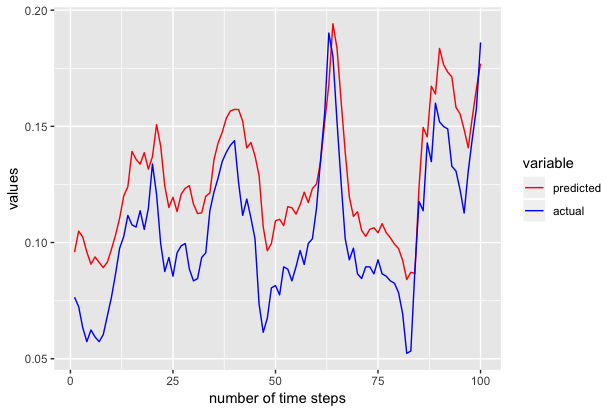
Now predicted contains the predicted 100 values. We use ggplot to plot the actual and predicted values as shown below.
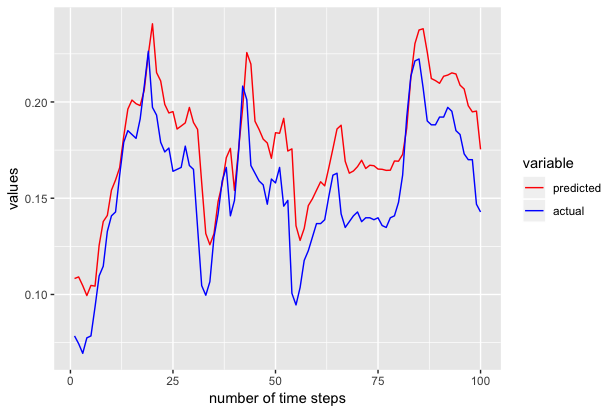
We also repeated the above experiments to generate the next 100 samples to 301st time series and we got the following results.
The above tutorial is just for demonstration purposes and has not been tuned extensively for accuracy.
For more tutorials on MXNet-R, head on to MXNet-R tutorials