\n", " \n", "
\n", "\n", "### Long Answer:\n", "\n", "All operators in MXNet have two methods defined: a `forward` method for executing the operator as expected, and a `backward` method that returns the partial derivative (the derivative of the output with respect to the input). On the vary rare occasion you need to implement your own custom operator, you'll define the same two methods.\n", "\n", "Automatic differentiation creates a record of the operators used (i.e. the `forward` method calls) by the network to make predictions and calculate the loss metric. A graph structure is used to record this, capturing the inputs (including their value) and outputs for each operator and how the operators are related. We call this the 'forward pass' of training.\n", "\n", "Automatic differentiation then works backwards through each operator of the graph, calling the `backward` method on each operator to calculate the partial derivative and calculate the gradient of the loss metric with respect to the operator's input (which could be parameters). Usually we work backwards from the loss metric, and hence calculate the gradients of the loss metric, but this can be done from any output. We call this the 'backward pass' of training.\n", "\n", "## What are the advantages of Automatic Differentiation (`autograd`)?\n", "\n", "### Short Answer:\n", "\n", "It's flexible, automatic and efficient. You can use native Python control flow operators such as `if` conditions and `while` loops and `autograd` will still be able to backpropogate the gradients correctly.\n", "\n", "### Long Answer:\n", "\n", "A huge benefit of using `autograd` is the flexibility it gives you when defining your network. You can change the operations on every iteration, and `autograd` will still be able to backpropogate the gradients correctly. You'll sometimes hear these called 'dynamic graphs', and are much more complex to implement in frameworks that require static graphs, such as TensorFlow.\n", "\n", "As suggested by the name, `autograd` is automatic and so the complexities of the backpropogation procedure are taken care of for you. All you have to do is tell `autograd` when you're interested in recording gradients, and specify what gradients you're interested in calculating: this will nearly always just be the gradient of the loss metric. And these gradient calculations will be performed efficiently too.\n", "\n", "## How do I use `autograd` in MXNet Gluon?\n", "\n", "Step one is to import the `autograd` package." ] }, { "cell_type": "markdown", "id": "e0629513", "metadata": {}, "source": [ "```\n", "from mxnet import autograd\n", "```\n" ] }, { "cell_type": "markdown", "id": "847b5c64", "metadata": {}, "source": [ "As a simple example, we'll implement the regression model shown in the diagrams above, and later use `autograd` to automatically calculate the gradient of the loss with respect to each of the weight parameters." ] }, { "cell_type": "markdown", "id": "dd73e1f4", "metadata": {}, "source": [ "```\n", "import mxnet as mx\n", "from mxnet.gluon.nn import HybridSequential, Dense\n", "from mxnet.gluon.loss import L2Loss\n", "\n", "\n", "# Define network\n", "net = HybridSequential()\n", "net.add(Dense(units=3))\n", "net.add(Dense(units=1))\n", "net.initialize()\n", "\n", "# Define loss\n", "loss_fn = L2Loss()\n", "\n", "# Create dummy data\n", "x = mx.nd.array([[0.3, 0.5]])\n", "y = mx.nd.array([[1.5]])\n", "```\n" ] }, { "cell_type": "markdown", "id": "cd9d8638", "metadata": {}, "source": [ "We're ready for our first forward pass through the network, and we want `autograd` to record the computational graph so we can calculate gradients. One of the simplest ways to do this is by running the network (and loss) code in the scope of an `autograd.record` context." ] }, { "cell_type": "markdown", "id": "d717132d", "metadata": {}, "source": [ "```\n", "with autograd.record():\n", " y_hat = net(x)\n", " loss = loss_fn(y_hat, y)\n", "```\n" ] }, { "cell_type": "markdown", "id": "805cd01c", "metadata": {}, "source": [ "Only operations that we want recorded are in the scope of the `autograd.record` context (since there is a computational overhead), and `autograd` should now have constructed a graph of these operations ready for the backward pass. We start the backward pass by calling the `backward` method on the quantity of interest, which in this case is `loss` since were trying to calculate the gradient of the loss with respect to the parameters.\n", "\n", "Remember: if `loss` isn't a single scalar value (e.g. could be a loss for each sample, rather than for whole batch) a `sum` operation will be applied implicitly before starting the backward propagation, and the gradients calculated will be of this `sum` with respect to the parameters." ] }, { "cell_type": "markdown", "id": "8ed8fbd5", "metadata": {}, "source": [ "```\n", "loss.backward()\n", "```\n" ] }, { "cell_type": "markdown", "id": "d23fd74e", "metadata": {}, "source": [ "And that's it! All the `autograd` magic is complete. We should now have gradients for each parameter of the network, which will be used by the optimizer to update the parameter values for improved performance. Check out the gradients of the first layer for example:" ] }, { "cell_type": "markdown", "id": "f65dd9fd", "metadata": {}, "source": [ "```\n", "net[0].weight.grad()\n", "```\n" ] }, { "cell_type": "markdown", "id": "a785a9db", "metadata": {}, "source": [ "## Advanced: Switching between training vs inference modes\n", "\n", "Some neural network layers behave differently depending on whether you're training the network or running it for inference. One example is `Dropout`, where activations are set to 0 at random during training, but remain unchanged during inference. Another is `BatchNorm`, where local batch statistics are used to normalize while training, but global statistics are used during inference.\n", "\n", "With MXNet Gluon, `autograd` is critical for switching between training and inference modes. As the default, networks will run in inference mode. While `autograd` is recording though, networks will run in training mode. Operations under the `autograd.record()` context scope are an example of this.\n", "\n", "Creating a network of a single `Dropout` block will demonstrate this." ] }, { "cell_type": "markdown", "id": "41d73be3", "metadata": {}, "source": [ "```\n", "dropout = mx.gluon.nn.Dropout(rate=0.5)\n", "data = mx.nd.ones(shape=(3,3))\n", "\n", "output = dropout(data)\n", "is_training = autograd.is_training()\n", "print('is_training:', is_training, output)\n", "```\n" ] }, { "cell_type": "markdown", "id": "7e159877", "metadata": {}, "source": [ "We called `dropout` when `autograd` wasn't recording, so our network was in inference mode and thus we didn't see any dropout of the input (i.e. it's still ones). We can confirm the current mode by calling `autograd.is_training()`." ] }, { "cell_type": "markdown", "id": "b977e150", "metadata": {}, "source": [ "```\n", "with autograd.record():\n", " output = dropout(data)\n", "print('is_training:', is_training, output)\n", "```\n" ] }, { "cell_type": "markdown", "id": "72f57150", "metadata": {}, "source": [ "We called `dropout` while `autograd` was recording this time, so our network was in training mode and we see dropout of the input this time. Since the probability of dropout was 50%, the output is automatically scaled by 1/0.5=2 to preserve the average activation.\n", "\n", "We can force some operators to behave as they would during training, even in inference mode. One example is setting `mode='always'` on the [Dropout](/api/python/ndarray/ndarray.html#mxnet.ndarray.Dropout) operator, but this usage is uncommon.\n", "\n", "## Advanced: Skipping the calculation of parameter gradients\n", "\n", "When creating neural networks with MXNet Gluon it is assumed that you're interested in the gradients of the loss with respect to each of the network's parameters. We're usually training the whole network, so this is exactly what we want. When we call `net.initialize()`, the network parameters get (lazily) initalized and memory is also allocated for the gradients, esentially doubling the space required for each parameter. After performing a forward and backward pass through the network, we will have gradients for all of the parameters.\n", "\n", "Sometimes we don't need the gradients for all of the parameters though. One example would be 'freezing' the values of the parameters in certain layers. Since we don't need to update the values, we don't need the gradients. Using the `grad_req` property of a parameter and setting it to `'null'`, we can indicate this to `autograd`, saving us computation time and memory." ] }, { "cell_type": "markdown", "id": "e4d9b946", "metadata": {}, "source": [ "```\n", "net[0].weight.grad_req = 'null'\n", "```\n" ] }, { "cell_type": "markdown", "id": "35932743", "metadata": {}, "source": [ "\n", " \n", "
\n", "\n", "## Advanced: Calculating non-parameter gradients\n", "\n", "Although it's most common to deal with network parameters (with `Parameter` being an MXNet Gluon abstraction), there are cases when you need to calculate the gradient with respect to thing that are not parameters (i.e. standard `ndarray`s). One example would be finding the gradient of the loss with respect to the input data to generate adversarial examples.\n", "\n", "With `autograd` it's simple, but there's one key difference compared to parameters: parameters are assumed to require gradients by default, non-parameters are not. We need to explicitly state that we require the gradient, and we do that by calling `.attach_grad()` on the `ndarray`. We can then access the gradient using `.grad` after the `backward` pass.\n", "\n", "As a simple example, let's take the case where $y=2x^2$ and use `autograd` to calculate gradient of $y$ with respect to $x$ at three different values of $x$. We could obviously work out the gradient by hand in this case as $dy/dx=4x$, but let's use this knowledge to check `autograd`. Given $x$ is an `ndarray` and not a `Parameter`, we need to call `x.attach_grad()`." ] }, { "cell_type": "markdown", "id": "f1af3d92", "metadata": {}, "source": [ "```\n", "x = mx.nd.array([1, 2, 3])\n", "x.attach_grad()\n", "with autograd.record():\n", " y = 2 * x ** 2\n", "y.backward()\n", "print(x.grad)\n", "```\n" ] }, { "cell_type": "markdown", "id": "596462b1", "metadata": {}, "source": [ "## Advanced: Using Python control flow\n", "\n", "As mentioned before, one of the main advantages of `autograd` is the ability to automatically calculate gradients of dynamic graphs (i.e. graphs where the operators could be different on every forward pass). One example of this would be applying a tree structured recurrent network to parse a sentence using its parse tree. And we can use Python control flow operators to create a dynamic flow that depends on the data, rather than using [MXNet's control flow operators](/api/python/docs/tutorials/packages/autograd/index.html#Advanced:-Using-Python-control-flow).\n", "\n", "We'll write a function as a toy example of a dynamic network. We'll add an `if` condition and a loop with a variable number of iterations, both of which will depend on the input data. Although these can now be used in static graphs (with conditional operators) it's still much more natural to use native control flow." ] }, { "cell_type": "markdown", "id": "f715cc41", "metadata": {}, "source": [ "```\n", "import math\n", "\n", "\n", "def f(x):\n", " y = x # going to change y but still want to use x\n", " if x < 0.75: # variable num_loops because it depends on x\n", " num_loops = math.floor(1/(1-x.asscalar()))\n", " for i in range(num_loops):\n", " y = y * x # increase polynomial degree\n", " else: # otherwise flatline\n", " y = y * 0\n", " return y\n", "```\n" ] }, { "cell_type": "markdown", "id": "71cd8a21", "metadata": {}, "source": [ "We can plot the resultant function for $x$ between 0 and 1, and we should recognise certain functions in segments of $x$. Starting with a quadratic curve from 0 to 1/2, we have a cubic curve from 1/2 to 2/3, a quartic from 2/3 to 3/4 and finally a flatline.\n", "\n", "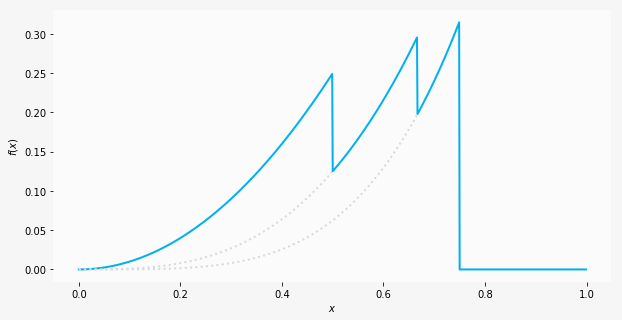\n", "\n", "Using `autograd`, let's now find the gradient of this arbritrary function. We don't have a vectorized function in this case, because of the control flow, so let's also create a function to calculate the gradient using `autograd`." ] }, { "cell_type": "markdown", "id": "dec2773b", "metadata": {}, "source": [ "```\n", "def get_grad(f, x):\n", " x.attach_grad()\n", " with autograd.record():\n", " y = f(x)\n", " y.backward()\n", " return x.grad\n", "\n", "xs = mx.nd.arange(0.0, 1.0, step=0.1)\n", "grads = [get_grad(f, x).asscalar() for x in xs]\n", "print(grads)\n", "```\n" ] }, { "cell_type": "markdown", "id": "56b330d4", "metadata": {}, "source": [ "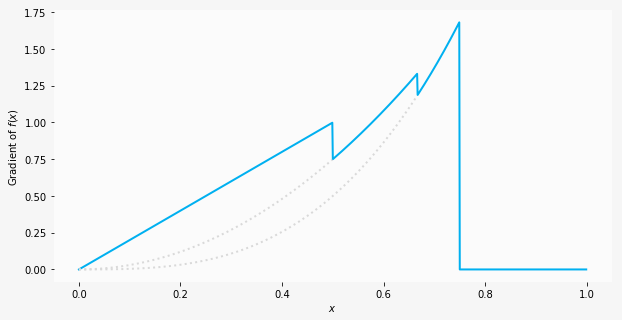\n", "\n", "We can calculate the gradients by hand in this situation (since it's a toy example), and for the four segments discussed before we'd expect $2x$, $3x^2$, $4x^3$ and 0. As a spot check, for $x=0.6$ the hand calculated gradient would be $3x^2=1.08$, which equals `1.08` as computed by `autograd`.\n", "\n", "\n", "## Advanced: Custom head gradients\n", "\n", "Most of the time `autograd` will be aware of the complete computational graph, and be able to calculate the gradients automatically. On a few rare occasions, you might have external post processing components (outside of MXNet Gluon) but still want to compute gradients with respect to MXNet Gluon network parameters.\n", "\n", "`autograd` enables this functionality by letting you pass in custom head gradients to `.backward()`. When nothing is specified (for the majority of cases), `autograd` will just used ones by default. Say we're interested in calculating $dz/dx$ but only calculate an intermediate variable $y$ using MXNet Gluon. We need to first calculate the head gradient $dz/dy$ (manually or otherwise), and then pass this to `.backward()`. `autograd` will then use this to calculate $dz/dx$, applying the chain rule.\n", "\n", "\n", " \n", "
\n", "\n", "As an example, let's take $y=x^3$ (calculated with `mxnet`) and $z=y^2$. (calculated with `numpy`). We can manually calculate $dz/dy=2y$ (once again with `numpy`), and use this as the head gradient for `autograd` to automatically calculate $dz/dx$. Applying the chain rule by hand we could calculate $dz/dx=6x^5$, so for $x=2$ we expect $dz/dx=192$. Let's check to see whether `autograd` calculates the same." ] }, { "cell_type": "markdown", "id": "9f2d9cde", "metadata": {}, "source": [ "```\n", "x = mx.nd.array([2,])\n", "x.attach_grad()\n", "# compute y inside of mxnet (with `autograd`)\n", "with autograd.record():\n", " y = x**3\n", "# compute dz/dy outside of mxnet\n", "y_np = y.asnumpy()\n", "z_np = y_np**2\n", "dzdy_np = 2*y_np\n", "# compute dz/dx inside of mxnet (given dz/dy)\n", "dzdy = mx.nd.array(dzdy_np)\n", "y.backward(dzdy)\n", "print(x.grad)\n", "```\n" ] }, { "cell_type": "markdown", "id": "09c08e38", "metadata": {}, "source": [ "And as expected, we get a gradient of 192 for `x`." ] } ], "metadata": { "language_info": { "name": "python" } }, "nbformat": 4, "nbformat_minor": 5 }