Develop a Neural Network with MXNet in Five Minutes¶

This tutorial is designed for new users of the mxnet package for R. It shows how to construct a neural network to do regression in 5 minutes. It shows how to perform classification and regression tasks, respectively. The data we use is in the mlbench package. Instructions to install R and MXNet’s R package in different environments can be found here.

Classification¶

   ## Loading required package: mlbench

    if (!require(mlbench)) {
      install.packages('mlbench')
    }

   ## Loading required package: mxnet

    require(mxnet)

   ## Loading required datasets

    data(Sonar, package="mlbench")

    Sonar[,61] = as.numeric(Sonar[,61])-1
    train.ind = c(1:50, 100:150)
    train.x = data.matrix(Sonar[train.ind, 1:60])
    train.y = Sonar[train.ind, 61]
    test.x = data.matrix(Sonar[-train.ind, 1:60])
    test.y = Sonar[-train.ind, 61]

We are going to use a multi-layer perceptron as our classifier. In mxnet, we have a function called mx.mlp for building a general multi-layer neural network to do classification or regression.

mx.mlp requires the following parameters:

Training data and label
Number of hidden nodes in each hidden layer
Number of nodes in the output layer
Type of the activation
Type of the output loss
The device to train (GPU or CPU)
Other parameters for mx.model.FeedForward.create

The following code shows an example usage of mx.mlp:

    mx.set.seed(0)
    model <- mx.mlp(train.x, train.y, hidden_node=10, out_node=2, out_activation="softmax",
                num.round=20, array.batch.size=15, learning.rate=0.07, momentum=0.9,
                eval.metric=mx.metric.accuracy)

   ## Auto detect layout of input matrix, use rowmajor..
   ## Start training with 1 devices
   ## [1] Train-accuracy=0.488888888888889
   ## [2] Train-accuracy=0.514285714285714
   ## [3] Train-accuracy=0.514285714285714
   ## [4] Train-accuracy=0.514285714285714
   ## [5] Train-accuracy=0.514285714285714
   ## [6] Train-accuracy=0.523809523809524
   ## [7] Train-accuracy=0.619047619047619
   ## [8] Train-accuracy=0.695238095238095
   ## [9] Train-accuracy=0.695238095238095
   ## [10] Train-accuracy=0.761904761904762
   ## [11] Train-accuracy=0.828571428571429
   ## [12] Train-accuracy=0.771428571428571
   ## [13] Train-accuracy=0.742857142857143
   ## [14] Train-accuracy=0.733333333333333
   ## [15] Train-accuracy=0.771428571428571
   ## [16] Train-accuracy=0.847619047619048
   ## [17] Train-accuracy=0.857142857142857
   ## [18] Train-accuracy=0.838095238095238
   ## [19] Train-accuracy=0.838095238095238
   ## [20] Train-accuracy=0.838095238095238

Note that mx.set.seed controls the random process in mxnet. You can see the accuracy in each round during training. It’s also easy to make predictions and evaluate.

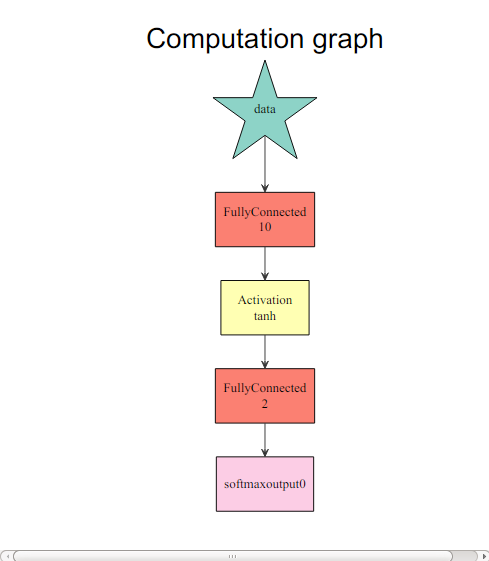
To get an idea of what is happening, view the computation graph from R:

    graph.viz(model$symbol)

    preds = predict(model, test.x)

   ## Auto detect layout of input matrix, use rowmajor.

    pred.label = max.col(t(preds))-1
    table(pred.label, test.y)

   ##           test.y
   ## pred.label  0  1
   ##          0 24 14
   ##          1 36 33

Note for that for multi-class predictions, mxnet outputs nclass x nexamples, with each row corresponding to the probability of the class.

Regression¶

Again, let us preprocess the data:

    data(BostonHousing, package="mlbench")

    train.ind = seq(1, 506, 3)
    train.x = data.matrix(BostonHousing[train.ind, -14])
    train.y = BostonHousing[train.ind, 14]
    test.x = data.matrix(BostonHousing[-train.ind, -14])
    test.y = BostonHousing[-train.ind, 14]

Although we can use mx.mlp again to do regression by changing the out_activation, this time we are going to introduce a flexible way to configure neural networks in mxnet. Configuration is done by the “Symbol” system in mxnet. The Symbol system takes care of the links among nodes, activation, dropout ratio, etc. Configure a multi-layer neural network as follows:

    # Define the input data
    data <- mx.symbol.Variable("data")
    # A fully connected hidden layer
    # data: input source
    # num_hidden: number of neurons in this hidden layer
    fc1 <- mx.symbol.FullyConnected(data, num_hidden=1)

    # Use linear regression for the output layer
    lro <- mx.symbol.LinearRegressionOutput(fc1)

What matters for a regression task is mainly the last function. It enables the new network to optimize for squared loss. Now let’s train on this simple data set. In this configuration, we dropped the hidden layer so that the input layer is directly connected to the output layer.

Next, make prediction with this structure and other parameters with mx.model.FeedForward.create:

    mx.set.seed(0)
    model <- mx.model.FeedForward.create(lro, X=train.x, y=train.y,
                                         ctx=mx.cpu(),     num.round=50, array.batch.size=20,
                                         learning.rate=2e-6, momentum=0.9,  eval.metric=mx.metric.rmse)

   ## Auto detect layout of input matrix, use rowmajor.
   ## Start training with 1 devices
   ## [1] Train-rmse=16.063282524034
   ## [2] Train-rmse=12.2792375712573
   ## [3] Train-rmse=11.1984634005885
   ## [4] Train-rmse=10.2645236892904
   ## [5] Train-rmse=9.49711005504284
   ## [6] Train-rmse=9.07733734175182
   ## [7] Train-rmse=9.07884450847991
   ## [8] Train-rmse=9.10463850277417
   ## [9] Train-rmse=9.03977049028532
   ## [10] Train-rmse=8.96870685004475
   ## [11] Train-rmse=8.93113287361574
   ## [12] Train-rmse=8.89937257821847
   ## [13] Train-rmse=8.87182096922953
   ## [14] Train-rmse=8.84476075083586
   ## [15] Train-rmse=8.81464673014974
   ## [16] Train-rmse=8.78672567900196
   ## [17] Train-rmse=8.76265872846474
   ## [18] Train-rmse=8.73946101419974
   ## [19] Train-rmse=8.71651926303267
   ## [20] Train-rmse=8.69457600919277
   ## [21] Train-rmse=8.67354928674563
   ## [22] Train-rmse=8.65328755392436
   ## [23] Train-rmse=8.63378039680078
   ## [24] Train-rmse=8.61488162586984
   ## [25] Train-rmse=8.5965105183022
   ## [26] Train-rmse=8.57868133563275
   ## [27] Train-rmse=8.56135851937663
   ## [28] Train-rmse=8.5444819772098
   ## [29] Train-rmse=8.52802114610432
   ## [30] Train-rmse=8.5119504512622
   ## [31] Train-rmse=8.49624261719241
   ## [32] Train-rmse=8.48087453238701
   ## [33] Train-rmse=8.46582689119887
   ## [34] Train-rmse=8.45107881002491
   ## [35] Train-rmse=8.43661331401712
   ## [36] Train-rmse=8.42241575909639
   ## [37] Train-rmse=8.40847217331365
   ## [38] Train-rmse=8.39476931796395
   ## [39] Train-rmse=8.38129658373974
   ## [40] Train-rmse=8.36804269059018
   ## [41] Train-rmse=8.35499817678397
   ## [42] Train-rmse=8.34215505742154
   ## [43] Train-rmse=8.32950441908131
   ## [44] Train-rmse=8.31703985777311
   ## [45] Train-rmse=8.30475363906755
   ## [46] Train-rmse=8.29264031506106
   ## [47] Train-rmse=8.28069372820073
   ## [48] Train-rmse=8.26890902770415
   ## [49] Train-rmse=8.25728089053853
   ## [50] Train-rmse=8.24580511500735

It’s also easy to make a prediction and evaluate it:

    preds = predict(model, test.x)

   ## Auto detect layout of input matrix, use rowmajor..

    sqrt(mean((preds-test.y)^2))

   ## [1] 7.800502

Currently, we have four predefined metrics: “accuracy”, “rmse”, “mae”, and “rmsle”. MXNet provides the interface for defining your own metrics:

    demo.metric.mae <- mx.metric.custom("mae", function(label, pred) {
      pred <- mx.nd.reshape(pred, shape = 0)
      res <- mx.nd.mean(mx.nd.abs(label-pred))
      return(res)
    })

This is an example of the mean absolute error metric. Simply plug it into the training function:

    mx.set.seed(0)
    model <- mx.model.FeedForward.create(lro, X=train.x, y=train.y,
                                         ctx=mx.cpu(),    num.round=50, array.batch.size=20,
                                         learning.rate=2e-6, momentum=0.9, eval.metric=demo.metric.mae)

   ## Auto detect layout of input matrix, use rowmajor.
   ## Start training with 1 devices
   ## [1] Train-mae=14.953625731998
   ## [2] Train-mae=11.4802955521478
   ## [3] Train-mae=8.50700579749213
   ## [4] Train-mae=7.30591265360514
   ## [5] Train-mae=7.38049803839789
   ## [6] Train-mae=7.36036252975464
   ## [7] Train-mae=7.06519222259521
   ## [8] Train-mae=6.9962231847975
   ## [9] Train-mae=6.96296903822157
   ## [10] Train-mae=6.9046172036065
   ## [11] Train-mae=6.87867620256212
   ## [12] Train-mae=6.85872554779053
   ## [13] Train-mae=6.81936407089233
   ## [14] Train-mae=6.79135354359945
   ## [15] Train-mae=6.77438741260105
   ## [16] Train-mae=6.75365140702989
   ## [17] Train-mae=6.73369296391805
   ## [18] Train-mae=6.71600982877943
   ## [19] Train-mae=6.69932826360067
   ## [20] Train-mae=6.6852519777086
   ## [21] Train-mae=6.67343420452542
   ## [22] Train-mae=6.66315894656711
   ## [23] Train-mae=6.65314838621351
   ## [24] Train-mae=6.64388704299927
   ## [25] Train-mae=6.63480265935262
   ## [26] Train-mae=6.62583245171441
   ## [27] Train-mae=6.61697626113892
   ## [28] Train-mae=6.60842116673787
   ## [29] Train-mae=6.60040124257406
   ## [30] Train-mae=6.59264140658908
   ## [31] Train-mae=6.58551020092434
   ## [32] Train-mae=6.57864215638902
   ## [33] Train-mae=6.57178926467896
   ## [34] Train-mae=6.56495311525133
   ## [35] Train-mae=6.55813185373942
   ## [36] Train-mae=6.5513252152337
   ## [37] Train-mae=6.54453214009603
   ## [38] Train-mae=6.53775374094645
   ## [39] Train-mae=6.53098879920112
   ## [40] Train-mae=6.52423816257053
   ## [41] Train-mae=6.51764053768582
   ## [42] Train-mae=6.51121346155802
   ## [43] Train-mae=6.5047902001275
   ## [44] Train-mae=6.49837123023139
   ## [45] Train-mae=6.49216641320123
   ## [46] Train-mae=6.48598252402412
   ## [47] Train-mae=6.4798010720147
   ## [48] Train-mae=6.47362396452162
   ## [49] Train-mae=6.46745183732775
   ## [50] Train-mae=6.46128723356459

Congratulations! You’ve learned the basics for using MXNet in R. To learn how to use MXNet’s advanced features, see the other tutorials.

Develop a Neural Network with MXNet in Five Minutes¶

Classification¶

Regression¶

Next Steps¶

Table Of Contents