Apache MXNet System Architecture
MXNet System Architecture
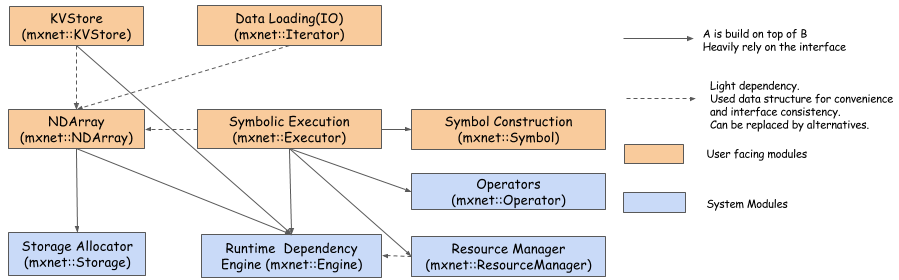
This figure shows the major modules and components of the MXNet system and their interaction. The modules are:
- Runtime Dependency Engine: Schedules and executes the operations according to their read/write dependency.
- Storage Allocator: Efficiently allocates and recycles memory blocks on host (CPU) and devices (GPUs).
- Resource Manager: Manages global resources, such as the random number generator and temporal space.
- NDArray: Dynamic, asynchronous n-dimensional arrays, which provide flexible imperative programs for MXNet.
- Symbolic Execution: Static symbolic graph executor, which provides efficient symbolic graph execution and optimization.
- Operator: Operators that define static forward and gradient calculation (backprop).
- SimpleOp: Operators that extend NDArray operators and symbolic operators in a unified fashion.
- Symbol Construction: Symbolic construction, which provides a way to construct a computation graph (net configuration).
- KVStore: Key-value store interface for efficient parameter synchronization.
- Data Loading(IO): Efficient distributed data loading and augmentation.
MXNet System Components
Execution Engine
You can use MXNet's engine not only for deep learning, but for any domain-specific problem. It's designed to solve a general problem: execute a bunch of functions following their dependencies. Execution of any two functions with dependencies should be serialized. To boost performance, functions with no dependencies can be executed in parallel. For a general discussion of this topic, see our notes on the dependency engine.
Interface
The following API is the core interface for the execution engine:
virtual void PushSync(Fn exec_fun, Context exec_ctx,
std::vector<VarHandle> const& const_vars,
std::vector<VarHandle> const& mutate_vars) = 0;
This API allows you to push a function (exec_fun),
along with its context information and dependencies, to the engine.
exec_ctx is the context information in which the exec_fun should be executed,
const_vars denotes the variables that the function reads from,
and mutate_vars are the variables to be modified.
The engine provides the following guarantee:
The execution of any two functions that modify a common variable is serialized in their push order.
Function
The function type of the engine is:
using Fn = std::function<void(RunContext)>;
RunContext contains runtime information, which is determined by the engine:
struct RunContext {
// stream pointer which could be safely cast to
// cudaStream_t* type
void *stream;
};
Alternatively, you could use mxnet::engine::DAGEngine::Fn, which has the same type definition.
All of the functions are executed by the engine's internal threads. In such a model, it's usually not a good idea to push blocking functions to the engine (usually for dealing with I/O tasks like disk, web service, UI, etc.) because it will occupy the execution thread and reduce total throughput. In that case, we provide another asynchronous function type:
using Callback = std::function<void()>;
using AsyncFn = std::function<void(RunContext, Callback)>;
In the AsyncFn function, you can pass the heavy part to your own threads
and safely exit the body of the function.
The engine doesn't consider the function finished
until the Callback function is called.
Context
You can specify the Context of the function to be executed within.
This usually includes whether the function should be run on a CPU or a GPU,
and if you specify a GPU, which GPU to use.
Context is different from RunContext.
Context contains device type (GPU/CPU) and device id,
while RunContext contains information that can be decided only during runtime,
for example, on which stream the function should be executed.
VarHandle
VarHandle is used to specify the dependencies of functions.
The MXNet engine is designed to be decoupled from other MXNet modules.
So VarHandle is like an engine-provided token you use
to represent the external resources the functions can use or modify.
It's designed to be lightweight, so creating,
deleting, or copying a variable incurs little overhead.
Upon pushing the functions, you need to specify the variables
that will be used (immutable) in the const_vars vector,
and the variables that will be modified (mutable) in the mutate_vars vector.
The engine uses one rule for resolving the dependencies among functions:
The execution of any two functions when one of them modifies at least one common variable is serialized in their push order.
For example, if Fn1 and Fn2 both mutate V2 then Fn2
is guaranteed to be executed after Fn1
if Fn2 is pushed after Fn1.
On the other hand, if Fn1 and Fn2 both use V2,
their actual execution order could be random.
This design allows the engine to schedule state-mutating operations in a manner
that minimizes calls to allocate new memory.
For example, the weight update function in DNN
can now use the += operator
to update the weights in place,
rather than generating a new weight array each time.
To create a variable, use the NewVar() API.
To delete a variable, use the PushDelete API.
Push and Wait
All Push APIs are asynchronous. The API call returns immediately
regardless of whether the pushed Fn is finished or not.
This allows the engine to start computing at the same time
as the user thread is pushing functions.
Push APIs are not thread-safe.
To be specific, only one thread should make engine API calls at a time.
If you want to wait for a specific Fn to finish,
include a callback function in the closure,
and call the function at the end of your Fn.
If you want to wait for all Fns
that involve (use or mutate) a certain variable to finish,
use the WaitForVar(var) API.
If you want to wait for all pushed Fns to finish,
use the WaitForAll() API.
Save Object Creation Cost
In some cases, you need to push several functions to the engine for a long period of time.
If the computation of these functions is light,
the overhead of copying lambdas and creating use/mutate variable lists becomes relatively high.
We provide an API to create an OprHandle beforehand:
virtual OprHandle NewOperator(AsyncFn fn,
std::vector<VarHandle> const& const_vars,
std::vector<VarHandle> const& mutate_vars) = 0;
You can keep pushing the OprHandle without repeatedly creating them:
virtual void Push(OprHandle op, Context exec_ctx) = 0;
To delete it, call the DeleteOperator(OprHandle op) API.
Ensure that the operator has finished computing before calling this API.
Operators in MXNet
In MXNet, an operator is a class that contains both actual computation logic
and auxiliary information that can aid the system in performing optimizations,
like in-place updates and auto-derivatives.
To understand the remainder of the document,
we recommend that you familiarize yourself with the mshadow library,
because all operators compute on the tensor-like structure mshadow::TBlob
provided by the system during runtime.
MXNet's operator interface allows you to:
- Reduce memory allocation cost by specifying in-place updates.
- Hide some internal arguments from Python to make it cleaner.
- Define the relationships among input tensors and output tensors, which allows the system to perform shape checking for you.
- Acquire additional temporary spaces from the system
to perform computation (e.g., calling
cudnnroutines).
Operator Interface
Forward is the core operator interface:
virtual void Forward(const OpContext &ctx,
const std::vector<TBlob> &in_data,
const std::vector<OpReqType> &req,
const std::vector<TBlob> &out_data,
const std::vector<TBlob> &aux_states) = 0;
The OpContext structure is:
struct OpContext {
int is_train;
RunContext run_ctx;
std::vector<Resource> requested;
}
It describes whether the operator is in the train or test phase,
which device the operator should be run on (in run_ctx),
and requested resources (covered in the following sections).
in_dataandout_datarepresent the input and output tensors, respectively. All of the tensor spaces have been allocated by the system.reqdenotes how the computation results are written into theout_data. In other words,req.size() == out_data.size()andreq[i]correspond to the write type ofout_data[i].The
OpReqTypeis defined as:
enum OpReqType {
kNullOp,
kWriteTo,
kWriteInplace,
kAddTo
};
Normally, the types of all out_data should be kWriteTo,
meaning that the provided out_data tensor is a raw memory block,
so the operator should write results directly into it.
In some cases, for example when calculating the gradient tensor,
it would be great if we could accumulate the result,
rather than directly overwrite the tensor contents
so that no extra space needs to be created each time.
In such a case, the corresponding req type is set as kAddTo,
indicating that a += should be called.
aux_statesis intentionally designed for auxiliary tensors used to help computation. Currently, it is useless.
Aside from the Forward operator, you could optionally implement the Backward interface:
virtual void Backward(const OpContext &ctx,
const std::vector<TBlob> &out_grad,
const std::vector<TBlob> &in_data,
const std::vector<TBlob> &out_data,
const std::vector<OpReqType> &req,
const std::vector<TBlob> &in_grad,
const std::vector<TBlob> &aux_states);
This interface follows the same design principle as the Forward interface,
except that out_grad, in_data, and out_data are given,
and the operator computes in_grad as the results.
The naming strategy is similar to Torch's convention,
and can be summarized in following figure:
[input/output semantics figure]
Some operators might not require all of the following:
out_grad, in_data and out_data.
You can specify these dependencies with the DeclareBackwardDependency interface in OperatorProperty.
Operator Property
One convolution might have several implementations,
and you might want to switch among them to achieve the best performance.
Therefore, we separate the operator semantic interfaces
from the implementation interface (Operator class)
into the OperatorProperty class.
The OperatorProperty interface consists of:
- InferShape:
virtual bool InferShape(mxnet::ShapeVector *in_shape,
mxnet::ShapeVector *out_shape,
mxnet::ShapeVector *aux_shape) const = 0;
This interface has two purposes:
* Tell the system the size of each input and output tensor,
so it can allocate space for them before the Forward and Backward call.
* Perform a size check to make sure that there isn't an obvious error before running.
The shape in in_shape is set by the system
(from the out_shape of the previous operators).
It returns false when there is not enough information
to infer shapes or throws an error when the shape is inconsistent.
- Request Resources: Operations like
cudnnConvolutionForwardneed a work space for computation. If the system can manage that, it could then perform optimizations, like reuse the space, and so on. MXNet defines two interfaces to achieve this:
virtual std::vector<ResourceRequest> ForwardResource(
const mxnet::ShapeVector &in_shape) const;
virtual std::vector<ResourceRequest> BackwardResource(
const mxnet::ShapeVector &in_shape) const;
The ResourceRequest structure (in resource.h) currently contains only a type flag:
struct ResourceRequest {
enum Type {
kRandom, // get a mshadow::Random<xpu> object
kTempSpace, // request temporary space
};
Type type;
};
If ForwardResource and BackwardResource return non-empty arrays,
the system offers the corresponding resources through the ctx parameter
in the Forward and Backward interface of Operator.
Basically, to access those resources, simply write:
auto tmp_space_res = ctx.requested[kTempSpace].get_space(some_shape, some_stream);
auto rand_res = ctx.requested[kRandom].get_random(some_stream);
For an example, see src/operator/cudnn_convolution-inl.h.
- Backward dependency: Let's look at two different operator signatures (we name all of the arguments for demonstration purposes):
void FullyConnectedForward(TBlob weight, TBlob in_data, TBlob out_data);
void FullyConnectedBackward(TBlob weight, TBlob in_data, TBlob out_grad, TBlob in_grad);
void PoolingForward(TBlob in_data, TBlob out_data);
void PoolingBackward(TBlob in_data, TBlob out_data, TBlob out_grad, TBlob in_grad);
Note that out_data in FullyConnectedForward
is not used by FullyConnectedBackward,
while PoolingBackward requires all of the arguments of PoolingForward.
Therefore, for FullyConnectedForward,
the out_data tensor once consumed could be safely freed
because the backward function will not need it.
This provides a chance for the system to collect some tensors
as garbage as soon as possible.
To specify this situation, we provide an interface:
virtual std::vector<int> DeclareBackwardDependency(
const std::vector<int> &out_grad,
const std::vector<int> &in_data,
const std::vector<int> &out_data) const;
The int element of the argument vector is an ID
to distinguish different arrays.
Let's see how this interface specifies different dependencies
for FullyConnected and Pooling:
std::vector<int> FullyConnectedProperty::DeclareBackwardDependency(
const std::vector<int> &out_grad,
const std::vector<int> &in_data,
const std::vector<int> &out_data) const {
return {out_grad[0], in_data[0]}; // NOTE: out_data[0] is NOT included
}
std::vector<int> PoolingProperty::DeclareBackwardDependency(
const std::vector<int> &out_grad,
const std::vector<int> &in_data,
const std::vector<int> &out_data) const {
return {out_grad[0], in_data[0], out_data[0]};
}
- In place Option: To further save the cost of memory allocation, you can use in-place updates. They are appropriate for element-wise operations when the input tensor and output tensor have the same shape. You specify and in-place update with the following interface:
virtual std::vector<std::pair<int, void*>> ElewiseOpProperty::ForwardInplaceOption(
const std::vector<int> &in_data,
const std::vector<void*> &out_data) const {
return { {in_data[0], out_data[0]} };
}
virtual std::vector<std::pair<int, void*>> ElewiseOpProperty::BackwardInplaceOption(
const std::vector<int> &out_grad,
const std::vector<int> &in_data,
const std::vector<int> &out_data,
const std::vector<void*> &in_grad) const {
return { {out_grad[0], in_grad[0]} }
}
This tells the system that the in_data[0] and out_data[0] tensors could share the same memory spaces during Forward, and so do out_grad[0] and in_grad[0] during Backward.
Important: Even if you use the preceding specification, it's not guaranteed that the input and output tensors will share the same space. In fact, this is only a suggestion for the system, which makes the final decision. However, in either case, the decision is completely transparent to you, so the actual
ForwardandBackwardimplementation does not need to consider that.
- Expose Operator to Python: Because of the restrictions of C++, you need user to implement following interfaces:
// initial the property class from a list of key-value string pairs
virtual void Init(const vector<pair<string, string>> &kwargs) = 0;
// return the parameters in a key-value string map
virtual map<string, string> GetParams() const = 0;
// return the name of arguments (for generating signature in python)
virtual vector<string> ListArguments() const;
// return the name of output values
virtual vector<string> ListOutputs() const;
// return the name of auxiliary states
virtual vector<string> ListAuxiliaryStates() const;
// return the number of output values
virtual int NumOutputs() const;
// return the number of visible outputs
virtual int NumVisibleOutputs() const;
Create an Operator from the Operator Property
OperatorProperty includes all semantic attributes of an operation. It's also responsible for creating the Operator pointer for actual computation.
Create Operator
Implement the following interface in OperatorProperty:
virtual Operator* CreateOperator(Context ctx) const = 0;
For example:
class ConvolutionOp {
public:
void Forward( ... ) { ... }
void Backward( ... ) { ... }
};
class ConvolutionOpProperty : public OperatorProperty {
public:
Operator* CreateOperator(Context ctx) const {
return new ConvolutionOp;
}
};
Parametrize Operator
When implementing a convolution operator, you need to know the kernel size,
the stride size, padding size, and so on.
These parameters should be passed to the operator
before any Forward or Backward interface is called.
To do so, you could define a ConvolutionParam structure, as follows:
#include <dmlc/parameter.h>
struct ConvolutionParam : public dmlc::Parameter<ConvolutionParam> {
mxnet::TShape kernel, stride, pad;
uint32_t num_filter, num_group, workspace;
bool no_bias;
};
Put it in ConvolutionOpProperty, and pass it to the operator class during construction:
class ConvolutionOp {
public:
ConvolutionOp(ConvolutionParam p): param_(p) {}
void Forward( ... ) { ... }
void Backward( ... ) { ... }
private:
ConvolutionParam param_;
};
class ConvolutionOpProperty : public OperatorProperty {
public:
void Init(const vector<pair<string, string>& kwargs) {
// initialize param_ using kwargs
}
Operator* CreateOperator(Context ctx) const {
return new ConvolutionOp(param_);
}
private:
ConvolutionParam param_;
};
Register the Operator Property Class and the Parameter Class to MXNet
Use the following macros to register the parameter structure and the operator property class to MXNet:
DMLC_REGISTER_PARAMETER(ConvolutionParam);
MXNET_REGISTER_OP_PROPERTY(Convolution, ConvolutionOpProperty);
The first argument is the name string, the second is the property class name.
Interface Summary
We've almost covered the entire interface required to define a new operator. Let's do a recap:
- Use the
Operatorinterface to write your computation logic (ForwardandBackward). - Use the
OperatorPropertyinterface to:- Pass the parameter to the operator class (you can use the
Initinterface). - Create an operator using the
CreateOperatorinterface. - Correctly implement the operator description interface, such as the names of arguments, etc.
- Correctly implement the
InferShapeinterface to set the output tensor shape. - [Optional] If additional resources are needed, check
ForwardResourceandBackwardResource. - [Optional] If
Backwarddoesn't need all of the input and output ofForward, checkDeclareBackwardDependency. - [Optional] If in-place update is supported, check
ForwardInplaceOptionandBackwardInplaceOption.
- Pass the parameter to the operator class (you can use the
- Register the
OperatorPropertyclass and the parameter class.
Unifying the NDArray Operator and Symbolic Operator
NDArray operations are similar to symbolic operations, except that sometimes you can't write in place to the operands without a complete dependency graph. However, the logic underlying NDArray and symbolic operations are almost identical. SimpleOp, a new unified operator API, unifies different invoking processes and returns to the fundamental elements of operators. Because most mathematical operators attend to one or two operands, and more operands make dependency-related optimization useful, the unified operator is specifically designed for unary and binary operations.
Consider the elements of an operation. Ideally, you need only functions and derivatives to describe an operation. Let's restrict that to the space of unary and binary operations. How do we classify all operations to maximize the possibility of in-place write optimization? Note that you can separate functions by the number of operands. Derivatives are a bit more complex. To construct a dependency graph, you need to know whether output value, input data, or neither are needed alongside head gradient. Gradient functions in the unified API are differentiated by the types of operands it takes for calculation.
Before you learn more about the SimpleOp interface,
we recommend that you review the
mshadow library guide
because calculations will be done in the mshadow::TBlob structure.
In the following example, we'll create an operator functioning as a smooth l1 loss, which is a mixture of l1 loss and l2 loss. The loss itself can be written as:
loss = outside_weight .* f(inside_weight .* (data - label))
grad = outside_weight .* inside_weight .* f'(inside_weight .* (data - label))
.* stands for element-wise multiplication, and f, f' is the smooth l1 loss function,
which we are assuming is in mshadow for now.
At first glance, it's impossible to implement
this particular loss as a unary or binary operator.
But we have automatic differentiation in symbolic execution.
That simplifies the loss to f and f' directly.
This loss is no more complex than a sin or an abs function,
and can certainly be implemented as a unary operator.
SimpleOp: The Unified Operator API
Define Shapes
The mshadow library requires explicit memory allocation.
As a consequence, all data shapes
must be provided before any calculation occurs.
Before we proceed with defining functions and gradient,
let's check input data shape consistency and provide output shape.
typedef mxnet::TShape (*UnaryShapeFunction)(const mxnet::TShape& src,
const EnvArguments& env);
typedef mxnet::TShape (*BinaryShapeFunction)(const mxnet::TShape& lhs,
const mxnet::TShape& rhs,
const EnvArguments& env);
You can use mshadow::TShape to check input data shape and designate output data shape.
If you don't define this function, the default output shape is the same as the input shape.
In the case of a binary operator, the shape of lhs and rhs is checked as the same by default.
You can also use shape functions to check if any additional arguments and resources are present.
Refer to the additional usages of EnvArguments to accomplish this.
Before we start on our smooth l1 loss example, we define a XPU to cpu or gpu in the header
smooth_l1_unary-inl.h implementation so that we reuse the same code in smooth_l1_unary.cc and
smooth_l1_unary.cu.
#include <mxnet/operator_util.h>
#if defined(__CUDACC__)
#define XPU gpu
#else
#define XPU cpu
#endif
In our smooth l1 loss example, it's okay to use the default behavior whereby the output has the same shape as the source. Written explicitly, it is:
inline mxnet::TShape SmoothL1Shape_(const mxnet::TShape& src,
const EnvArguments& env) {
return mxnet::TShape(src);
}
Define Functions
Create a unary or binary function with one output: mshadow::TBlob.
typedef void (*UnaryFunction)(const TBlob& src,
const EnvArguments& env,
TBlob* ret,
OpReqType req,
RunContext ctx);
typedef void (*BinaryFunction)(const TBlob& lhs,
const TBlob& rhs,
const EnvArguments& env,
TBlob* ret,
OpReqType req,
RunContext ctx);
- Functions are differentiated by the types of input arguments.
RunContext ctxcontains information needed during runtime for execution.
struct RunContext {
void *stream; // the stream of the device, can be NULL or Stream<gpu>* in GPU mode
template<typename xpu> inline mshadow::Stream<xpu>* get_stream() // get mshadow stream from Context
} // namespace mxnet
mshadow::stream<xpu> *s = ctx.get_stream<xpu>(); is an example of obtaining a stream from ctx.
* OpReqType req denotes how computation results are written into ret.
enum OpReqType {
kNullOp, // no operation, do not write anything
kWriteTo, // write gradient to provided space
kWriteInplace, // perform an in-place write
kAddTo // add to the provided space
};
A macro is defined in operator_util.h for a simplified use of OpReqType.
ASSIGN_DISPATCH(out, req, exp) checks req and performs an assignment.
In our smooth l1 loss example, we use UnaryFunction to define the function of this operator.
template<typename xpu>
void SmoothL1Forward_(const TBlob& src,
const EnvArguments& env,
TBlob *ret,
OpReqType req,
RunContext ctx) {
using namespace mshadow;
using namespace mshadow::expr;
mshadow::Stream<xpu> *s = ctx.get_stream<xpu>();
real_t sigma2 = env.scalar * env.scalar;
MSHADOW_TYPE_SWITCH(ret->type_flag_, DType, {
mshadow::Tensor<xpu, 2, DType> out = ret->get<xpu, 2, DType>(s);
mshadow::Tensor<xpu, 2, DType> in = src.get<xpu, 2, DType>(s);
ASSIGN_DISPATCH(out, req,
F<mshadow_op::smooth_l1_loss>(in, ScalarExp<DType>(sigma2)));
});
}
After obtaining mshadow::Stream from RunContext, we get mshadow::Tensor from mshadow::TBlob.
mshadow::F is a shortcut to initiate a mshadow expression. The macro MSHADOW_TYPE_SWITCH(type, DType, ...)
handles details on different types, and the macro ASSIGN_DISPATCH(out, req, exp) checks OpReqType and
performs actions accordingly. sigma2 is a special parameter in this loss, which we will cover later.
Define Gradients (Optional)
Create a gradient function with various types of inputs.
// depending only on out_grad
typedef void (*UnaryGradFunctionT0)(const OutputGrad& out_grad,
const EnvArguments& env,
TBlob* in_grad,
OpReqType req,
RunContext ctx);
// depending only on out_value
typedef void (*UnaryGradFunctionT1)(const OutputGrad& out_grad,
const OutputValue& out_value,
const EnvArguments& env,
TBlob* in_grad,
OpReqType req,
RunContext ctx);
// depending only on in_data
typedef void (*UnaryGradFunctionT2)(const OutputGrad& out_grad,
const Input0& in_data0,
const EnvArguments& env,
TBlob* in_grad,
OpReqType req,
RunContext ctx);
Gradient functions of binary operators have similar structures, except that Input, TBlob, and OpReqType
are doubled.
GradFunctionArgument
Input0, Input, OutputValue, and OutputGrad all share the structure of GradFunctionArgument,
which is defined as:
struct GradFunctionArgument {
TBlob data;
}
In our smooth l1 loss example, note that it's an f'(x),
which utilizes input for the gradient calculation,
so the UnaryGradFunctionT2 is suitable.
To enable the chain rule of the gradient,
we also need to multiply out_grad from the top to the result of in_grad.
template<typename xpu>
void SmoothL1BackwardUseIn_(const OutputGrad& out_grad,
const Input0& in_data0,
const EnvArguments& env,
TBlob *in_grad,
OpReqType req,
RunContext ctx) {
using namespace mshadow;
using namespace mshadow::expr;
mshadow::Stream<xpu> *s = ctx.get_stream<xpu>();
real_t sigma2 = env.scalar * env.scalar;
MSHADOW_TYPE_SWITCH(in_grad->type_flag_, DType, {
mshadow::Tensor<xpu, 2, DType> src = in_data0.data.get<xpu, 2, DType>(s);
mshadow::Tensor<xpu, 2, DType> ograd = out_grad.data.get<xpu, 2, DType>(s);
mshadow::Tensor<xpu, 2, DType> igrad = in_grad->get<xpu, 2, DType>(s);
ASSIGN_DISPATCH(igrad, req,
ograd * F<mshadow_op::smooth_l1_gradient>(src, ScalarExp<DType>(sigma2)));
});
}
Register SimpleOp to MXNet
After creating the shape, function, and gradient, restore them into both an NDArray operator and
a symbolic operator. To simplify this process, use the registration macro defined in operator_util.h.
MXNET_REGISTER_SIMPLE_OP(Name, DEV)
.set_shape_function(Shape)
.set_function(DEV::kDevMask, Function<XPU>, SimpleOpInplaceOption)
.set_gradient(DEV::kDevMask, Gradient<XPU>, SimpleOpInplaceOption)
.describe("description");
SimpleOpInplaceOption is defined as:
enum SimpleOpInplaceOption {
kNoInplace, // do not allow inplace in arguments
kInplaceInOut, // allow inplace in with out (unary)
kInplaceOutIn, // allow inplace out_grad with in_grad (unary)
kInplaceLhsOut, // allow inplace left operand with out (binary)
kInplaceOutLhs // allow inplace out_grad with lhs_grad (binary)
};
In our example, we have a gradient function that relies on input data, so the function can't be written in place. The output gradient has no purpose after gradient computation, so the gradient can be written in place.
MXNET_REGISTER_SIMPLE_OP(smooth_l1, XPU)
.set_function(XPU::kDevMask, SmoothL1Forward_<XPU>, kNoInplace)
.set_gradient(XPU::kDevMask, SmoothL1BackwardUseIn_<XPU>, kInplaceOutIn)
.set_enable_scalar(true)
.describe("Calculate Smooth L1 Loss(lhs, scalar)");
Remember from the discussion of shape functions that a default behavior without set_shape_function forces the inputs
(if they're binary) to be the same shape and yield the same shape for output. We'll discuss set_enable_scalar later.
NDArray Operator Summary
- Create a shape function for determining the output shape.
- Create a function as the forward routine by choosing a suitable function type.
- Create a gradient as the backward routine by choosing a suitable gradient type.
- Register the operator using the registration process.
Additional Information on SimpleOp
Using SimpleOp on EnvArguments
Some operations might need a scalar as input, such as a gradient scale, a set of keyword arguments
controlling behavior, or a temporary space to speed up calculations.EnvArguments provides additional arguments and resources to make calculations more scalable
and efficient.
struct EnvArguments {
real_t scalar; // scalar argument, if enabled
std::vector<std::pair<std::string, std::string> > kwargs; // keyword arguments
std::vector<Resource> resource; // pointer to the resources requested
};
More registration parameters are required to enable these additional features. To prevent confusion on parameters, scalar and kwargs
can't be present at the same time. To enable scalar, use
set_enable_scalar(bool enable_scalar) in registration. Then, in forward functions and gradients, the scalar can be accessed from env.scalar as in the function parameter EnvArguments env.
To enable kwargs, use set_enable_kwargs(bool enable_kwargs) in registration. Then, in forward
functions and gradients, additional arguments are contained in env.kwarg, which is defined as
std::vector<std::pair<std::string, std::string> >. Use the DMLC parameter structure to
simplify parsing keyword arguments. For more details, see the guide on parameter structure.
Additional resources like mshadow::Random<xpu> and temporary memory space can also be requested and
accessed from EnvArguments.resource. The registration routine is set_resource_request(ResourceRequest req)
or set_resource_request(const std::vector<ResourceRequest>), where mxnet::ResourceRequest is defined as:
struct ResourceRequest {
enum Type { // Resource type, indicating what the pointer type is
kRandom, // mshadow::Random<xpu> object
kTempSpace // A dynamic temp space that can be arbitrary size
};
Type type; // type of resources
};
Registration will request the declared resource requests from mxnet::ResourceManager, and place resources
in std::vector<Resource> resource in EnvArguments. To access resources, use the following:
auto tmp_space_res = env.resources[0].get_space(some_shape, some_stream);
auto rand_res = env.resources[0].get_random(some_stream);
For an example, see src/operator/loss_binary_op-inl.h.
In our smooth l1 loss example, a scalar input is needed to mark the turning point of a loss function. Therefore,
in the registration process, we use set_enable_scalar(true), and use env.scalar in function and gradient
declarations.
Crafting a Tensor Operation
Because computation utilizes the mshadow library and we sometimes don't have functions readily available, we
can craft tensor operations in operator implementations. If you define such functions as element-wise, you
can implement them as a mxnet::op::mshadow_op. src/operator/mshadow_op.h that contains a lot of mshadow_op,
for example. mshadow_op are expression mappers. They deal with the scalar case of desired functions. For details, see
mshadow expression API guide.
If an operation can't be done in an element-wise way, like the softmax loss and gradient, then you need to create a new tensor operation. You need to create as mshadow function and as mshadow::cuda
function directly. For details, see the mshadow library. For an example, see src/operator/roi_pooling.cc.
In our smooth l1 loss example, we create two mappers, namely the scalar cases of smooth l1 loss and gradient.
namespace mshadow_op {
struct smooth_l1_loss {
// a is x, b is sigma2
MSHADOW_XINLINE static real_t Map(real_t a, real_t b) {
if (a > 1.0f / b) {
return a - 0.5f / b;
} else if (a < -1.0f / b) {
return -a - 0.5f / b;
} else {
return 0.5f * a * a * b;
}
}
};
}
The gradient, which can be found in src/operator/smooth_l1_unary-inl.h, is similar.
Beyond Two Operands
The new unified API is designed to fulfill the fundamentals of an operation. For operators with more than two inputs, more than one output, or that need more features, see the original Operator API.
