Deep Learning Programming Paradigm
Deep Learning Programming Paradigm
However much we might ultimately care about performance, we first need working code before we can start worrying about optimization. Writing clear, intuitive deep learning code can be challenging, and the first thing any practitioner must deal with is the language syntax itself. Complicating matters, of the many deep learning libraries out there, each has its own approach to programming style.
In this document, we focus on two of the most important high-level design decisions: 1. Whether to embrace the symbolic or imperative paradigm for mathematical computation. 2. Whether to build networks with bigger (more abstract) or more atomic operations.
Throughout, we'll focus on the programming models themselves. When programming style decisions may impact performance, we point this out, but we don't dwell on specific implementation details.
Symbolic vs. Imperative Programs
If you are a Python or C++ programmer, then you're already familiar with imperative programs. Imperative-style programs perform computation as you run them. Most code you write in Python is imperative, as is the following NumPy snippet.
import numpy as np
a = np.ones(10)
b = np.ones(10) * 2
c = b * a
d = c + 1
When the program executes c = b * a, it runs the actual numerical computation.
Symbolic programs are a bit different. With symbolic-style programs, we first define a (potentially complex) function abstractly. When defining the function, no actual numerical computation takes place. We define the abstract function in terms of placeholder values. Then we can compile the function, and evaluate it given real inputs. In the following example, we rewrite the imperative program from above as a symbolic-style program:
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
# compiles the function
f = compile(D)
d = f(A=np.ones(10), B=np.ones(10)*2)
As you can see, in the symbolic version, when C = B * A is executed, no computation occurs.
Instead, this operation generates a computation graph (also called a symbolic graph)
that represents the computation.
The following figure shows a computation graph to compute D.
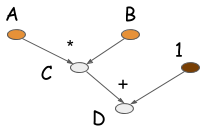
Most symbolic-style programs contain, either explicitly or implicitly, a compile step. This converts the computation graph into a function that we can later call. In the above example, numerical computation only occurs in the last line of code. The defining characteristic of symbolic programs is their clear separation between building the computation graph and executing it. For neural networks, we typically define the entire model as a single compute graph.
Among other popular deep learning libraries, Torch, Chainer, and Minerva embrace the imperative style. Examples of symbolic-style deep learning libraries include Theano, CGT, and TensorFlow. We might also view libraries like CXXNet and Caffe, which rely on configuration files, as symbolic-style libraries. In this interpretation, we'd consider the content of the configuration file as defining the computation graph.
Now that you understand the difference between these two programming models, let's compare the advantages of each.
Imperative Programs Tend to be More Flexible
When you're using an imperative-style library from Python, you are writing in Python. Nearly anything that would be intuitive to write in Python, you could accelerate by calling down in the appropriate places to the imperative deep learning library. On the other hand, when you write a symbolic program, you may not have access to all the familiar Python constructs, like iteration. Consider the following imperative program, and think about how you can translate this into a symbolic program.
a = 2
b = a + 1
d = np.zeros(10)
for i in range(d):
d += np.zeros(10)
This wouldn't be so easy if the Python for-loop weren't supported by the symbolic API. When you write a symbolic program in Python, you're not writing in Python. Instead, you're writing in a domain-specific language (DSL) defined by the symbolic API. The symbolic APIs found in deep learning libraries are powerful DSLs that generate callable computation graphs for neural networks. <!-- In that sense, config-file input libraries are all symbolic. -->
Intuitively, you might say that imperative programs are more native than symbolic programs. It's easier to use native language features. For example, it's straightforward to print out the values in the middle of computation or to use native control flow and loops at any point in the flow of computation.
Symbolic Programs Tend to be More Efficient
As we've seen, imperative programs tend to be flexible and fit nicely into the programming flow of a host language. So you might wonder, why do so many deep learning libraries embrace the symbolic paradigm? The main reason is efficiency, both in terms of memory and speed. Let's revisit our toy example from before.
import numpy as np
a = np.ones(10)
b = np.ones(10) * 2
c = b * a
d = c + 1
...

Assume that each cell in the array occupies 8 bytes of memory. How much memory do you need to execute this program in the Python console?
As an imperative program we need to allocate memory at each line.
That leaves us allocating 4 arrays of size 10.
So we'll need 4 * 10 * 8 = 320 bytes.
On the other hand, if we built a computation graph,
and knew in advance that we only needed d,
we could reuse the memory originally allocated for intermediate values.
For example, by performing computations in-place,
we might recycle the bits allocated for b to store c.
And we might recycle the bits allocated for c to store d.
In the end we could cut our memory requirement in half,
requiring just 2 * 10 * 8 = 160 bytes.
Symbolic programs are more restricted.
When we call compile on D, we tell the system
that only the value of d is needed.
The intermediate values of the computation,
in this case c, is then invisible to us.
We benefit because the symbolic programs
can then safely reuse the memory for in-place computation.
But on the other hand, if we later decide that we need to access c, we're out of luck.
So imperative programs are better prepared to encounter all possible demands.
If we ran the imperative version of the code in a Python console,
we could inspect any of the intermediate variables in the future.
Symbolic programs can also perform another kind of optimization, called operation folding. Returning to our toy example, the multiplication and addition operations can be folded into one operation, as shown in the following graph. If the computation runs on a GPU processor, one GPU kernel will be executed, instead of two. In fact, this is one way we hand-craft operations in optimized libraries, such as CXXNet and Caffe. Operation folding improves computation efficiency.
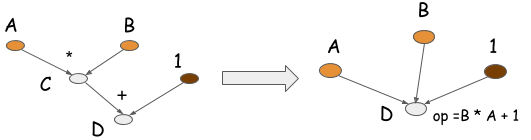
Note, you can't perform operation folding in imperative programs, because the intermediate values might be referenced in the future. Operation folding is possible in symbolic programs because you get the entire computation graph, and a clear specification of which values will be needed and which are not.
Case Study: Backprop and AutoDiff
In this section, we compare the two programming models on the problem of auto differentiation, or backpropagation. Differentiation is of vital importance in deep learning because it's the mechanism by which we train our models. In any deep learning model, we define a loss function. A loss function measures how far the model is from the desired output. We then typically pass over training examples (pairs of inputs and ground-truth outputs). At each step we update the model's parameters to minimize the loss. To determine the direction in which to update the parameters, we need to take the derivative of the loss function with respect to the parameters.
In the past, whenever someone defined a new model, they had to work out the derivative calculations by hand. While the math is reasonably straightforward, for complex models, it can be time-consuming and tedious work. All modern deep learning libraries make the practitioner/researcher's job much easier, by automatically solving the problem of gradient calculation.
Both imperative and symbolic programs can perform gradient calculation. So let's take a look at how you might perform automatic differentiation with each.
Let's start with imperative programs. The following example Python code performs automatic differentiation using our toy example:
class array(object) :
"""Simple Array object that support autodiff."""
def __init__(self, value, name=None):
self.value = value
if name:
self.grad = lambda g : {name : g}
def __add__(self, other):
assert isinstance(other, int)
ret = array(self.value + other)
ret.grad = lambda g : self.grad(g)
return ret
def __mul__(self, other):
assert isinstance(other, array)
ret = array(self.value * other.value)
def grad(g):
x = self.grad(g * other.value)
x.update(other.grad(g * self.value))
return x
ret.grad = grad
return ret
# some examples
a = array(1, 'a')
b = array(2, 'b')
c = b * a
d = c + 1
print d.value
print d.grad(1)
# Results
# 3
# {'a': 2, 'b': 1}
In this code, each array object contains a grad function (it is actually a closure).
When you run d.grad, it recursively invokes the grad function of its inputs,
backprops the gradient value back, and
returns the gradient value of each input.
This might look a bit complicated, so let's consider the gradient calculation for symbolic programs. The following program performs symbolic gradient calculation for the same task.
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
# get gradient node.
gA, gB = D.grad(wrt=[A, B])
# compiles the gradient function.
f = compile([gA, gB])
grad_a, grad_b = f(A=np.ones(10), B=np.ones(10)*2)
The grad function of D generates a backward computation graph,
and returns a gradient node, gA, gB,
which correspond to the red nodes in the following figure.

The imperative program actually does the same thing as the symbolic program.
It implicitly saves a backward computation graph in the grad closure.
When you invoked d.grad, you start from d(D),
backtrack through the graph to compute the gradient, and collect the results.
The gradient calculations in both symbolic
and imperative programming follow the same pattern.
What's the difference then?
Recall the be prepared to encounter all possible demands requirement of imperative programs.
If you are creating an array library that supports automatic differentiation,
you have to keep the grad closure along with the computation.
This means that none of the history variables can be
garbage-collected because they are referenced by variable d by way of function closure.
What if you want to compute only the value of d,
and don't want the gradient value?
In symbolic programming, you declare this with f=compiled([D]).
This also declares the boundary of computation,
telling the system that you want to compute only the forward pass.
As a result, the system can free the memory of previous results,
and share the memory between inputs and outputs.
Imagine running a deep neural network with n layers.
If you are running only the forward pass,
not the backward(gradient) pass,
you need to allocate only two copies of
temporal space to store the values of the intermediate layers,
instead of n copies of them.
However, because imperative programs need to be prepared
to encounter all possible demands of getting the gradient,
they have to store the intermediate values,
which requires n copies of temporal space.
As you can see, the level of optimization depends on the restrictions on what you can do. Symbolic programs ask you to clearly specify these restrictions when you compile the graph. One the other hand, imperative programs must be prepared for a wider range of demands. Symbolic programs have a natural advantage because they know more about what you do and don't want.
There are ways in which we can modify imperative programs to incorporate similar restrictions. For example, one solution to the preceding problem is to introduce a context variable. You can introduce a no-gradient context variable to turn gradient calculation off.
with context.NoGradient():
a = array(1, 'a')
b = array(2, 'b')
c = b * a
d = c + 1
However, this example still must be prepared to encounter all possible demands, which means that you can't perform the in-place calculation to reuse memory in the forward pass (a trick commonly used to reduce GPU memory usage). The techniques we've discussed generate an explicit backward pass. Some of the libraries such as Caffe and CXXNet perform backprop implicitly on the same graph. The approach we've discussed in this section also applies to them.
Most configuration-file-based libraries, such as CXXNet and Caffe are designed to meet one or two generic requirements: get the activation of each layer, or get the gradient of all of the weights. These libraries have the same problem: the more generic operations the library has to support, the less optimization (memory sharing) you can do, based on the same data structure.
As you can see, the trade-off between restriction and flexibility is the same for most cases.
Model Checkpoint
It's important to able to save a model and load it back later. There are different ways to save your work. Normally, to save a neural network, you need to save two things: a net configuration for the structure of the neural network and the weights of the neural network.
The ability to check the configuration is a plus for symbolic programs. Because the symbolic construction phase does not perform computation, you can directly serialize the computation graph, and load it back later. This solves the problem of saving the configuration without introducing an additional layer.
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
D.save('mygraph')
...
D2 = load('mygraph')
f = compile([D2])
# more operations
...
Because an imperative program executes as it describes the computation,
you have to save the code itself as the configuration,
or build another configuration layer on top of the imperative language.
Parameter Updates
Most symbolic programs are data flow (computation) graphs. Data flow graphs describe computation. But it's not obvious how to use graphs to describe parameter updates. That's because parameter updates introduce mutation, which is not a data flow concept. Most symbolic programs introduce a special update statement to update persistent state in the programs.
It's usually easier to write parameter updates in an imperative style, especially when you need multiple updates that relate to each other. For symbolic programs, the update statement is also executed as you call it. So in that sense, most symbolic deep learning libraries fall back on the imperative approach to perform updates, while using the symbolic approach to perform gradient calculation.
There Is No Strict Boundary
In comparing the two programming styles, some of our arguments might not be strictly true, i.e., it's possible to make an imperative program more like a traditional symbolic program or vice versa. However, the two archetypes are useful abstractions, especially for understanding the differences between deep learning libraries. We might reasonably conclude that there is no clear boundary between programming styles. For example, you can create a just-in-time (JIT) compiler in Python to compile imperative Python programs, which provides some of the advantages of global information held in symbolic programs.
Big vs. Small Operations
When designing a deep learning library, another important programming model decision is precisely what operations to support. In general, there are two families of operations supported by most deep learning libraries:
- Big operations - typically for computing neural network layers (e.g. FullyConnected and BatchNormalize).
- Small operations - mathematical functions like matrix multiplication and element-wise addition.
Libraries like CXXNet and Caffe support layer-level operations. Libraries like Theano and Minerva support fine-grained operations.
Smaller Operations Can Be More Flexible
It's quite natural to use smaller operations to compose bigger operations. For example, the sigmoid unit can simply be composed of division, addition and an exponentiation:
sigmoid(x) = 1.0 / (1.0 + exp(-x))
Using smaller operations as building blocks, you can express nearly anything you want. If you're more familiar with CXXNet- or Caffe-style layers, note that these operations don't differ from a layer, except that they are smaller.
SigmoidLayer(x) = EWiseDivisionLayer(1.0, AddScalarLayer(ExpLayer(-x), 1.0))
This expression composes three layers, with each defining its forward and backward (gradient) function. Using smaller operations gives you the advantage of building new layers quickly, because you only need to compose the components.
Big Operations Are More Efficient
Directly composing sigmoid layers requires three layers of operation, instead of one.
SigmoidLayer(x) = EWiseDivisionLayer(1.0, AddScalarLayer(ExpLayer(-x), 1.0))
This code creates overhead for computation and memory (which could be optimized, with cost).
Libraries like CXXNet and Caffe take a different approach. To support coarse-grained operations, such as BatchNormalization and the SigmoidLayer directly, in each layer, the calculation kernel is hand crafted with one or only some CUDA kernel launches. This makes these implementations more efficient.
Compilation and Optimization
Can small operations be optimized? Of course, they can. Let's look at the system optimization part of the compilation engine. Two types of optimization can be performed on the computation graph:
- Memory allocation optimization, to reuse the memory of the intermediate computations.
- Operator fusion, to detect sub-graph patterns, such as the sigmoid, and fuse them into a bigger operation kernel.
Memory allocation optimization isn't restricted to small operations graphs.
You can use it with bigger operations graph, too.
However, optimization might not be essential
for bigger operation libraries like CXXNet and Caffe,
because you can't find the compilation step in them.
However, there's a (dumb) compilation step in these libraries,
that basically translates the layers into a fixed forward,
backprop execution plan, by running each operation one by one.
For computation graphs with smaller operations, these optimizations are crucial to performance. Because the operations are small, there are many sub-graph patterns that can be matched. Also, because the final, generated operations might not be enumerable, an explicit recompilation of the kernels is required, as opposed to the fixed amount of precompiled kernels in the big operation libraries. This creates compilation overhead for the symbolic libraries that support small operations. Requiring compilation optimization also creates engineering overhead for the libraries that solely support smaller operations.
As in the case of symbolic vs. imperative, the bigger operation libraries "cheat" by asking you to provide restrictions (to the common layer), so that you actually perform the sub-graph matching. This moves the compilation overhead to the real brain, which is usually not too bad.
Expression Template and Statically Typed Language
You always have a need to write small operations and compose them. Libraries like Caffe use hand-crafted kernels to build these bigger blocks. Otherwise, you would have to compose smaller operations using Python.
There's a third choice that works pretty well. This is called the expression template. Basically, you use template programming to generate generic kernels from an expression tree at compile time. For details, see Expression Template Tutorial. CXXNet makes extensive use of an expression template, which enables creating much shorter and more readable code that matches the performance of hand-crafted kernels.
The difference between using an expression template and Python kernel generation is that expression evaluation is done at compile time for C++ with an existing type, so there is no additional runtime overhead. In principle, this is also possible with other statically typed languages that support templates, but we've seen this trick used only in C++.
Expression template libraries create a middle ground between Python operations and hand-crafted big kernels by allowing C++ users to craft efficient big operations by composing smaller operations. It's an option worth considering.
Mix the Approaches
Now that we've compared the programming models, which one should you choose? Before delving into that, we should emphasize that depending on the problems you're trying to solve, our comparison might not necessarily have a big impact.
Remember Amdahl's law: If you are optimizing a non-performance-critical part of your problem, you won't get much of a performance gain.
As you've seen, there usually is a trade-off between efficiency, flexibility, and engineering complexity. The more suitable programming style depends on the problem you are trying to solve. For example, imperative programs are better for parameter updates, and symbolic programs for gradient calculation.
We advocate mixing the approaches. Sometimes the part that we want to be flexible isn't crucial to performance. In these cases, it's okay to leave some efficiency on the table to support more flexible interfaces. In machine learning, combining methods usually works better than using just one.
If you can combine the programming models correctly, you can get better results than when using a single programming model. In this section, we discuss how to do so.
Symbolic and Imperative Programs
There are two ways to mix symbolic and imperative programs:
- Use imperative programs within symbolic programs as callbacks
- Use symbolic programs as part of imperative programs
We've observed that it's usually helpful to write parameter updates imperatively, and perform gradient calculations in symbolic programs.
Symbolic libraries already mix programs because Python itself is imperative. For example, the following program mixes the symbolic approach with NumPy, which is imperative.
A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
# compiles the function
f = compile(D)
d = f(A=np.ones(10), B=np.ones(10)*2)
d = d + 1.0
The symbolic graphs are compiled into a function that can be executed imperatively. The internals are a black box to the user. This is exactly like writing C++ programs and exposing them to Python, which we commonly do.
Because parameter memory resides on the GPU, you might not want to use NumPy as an imperative component. Supporting a GPU-compatible imperative library that interacts with symbolic compiled functions or provides a limited amount of updating syntax in the update statement in symbolic program execution might be a better choice.
Small and Big Operations
There might be a good reason to combine small and big operations. Consider applications that perform tasks such as changing a loss function or adding a few customized layers to an existing structure. Usually, you can use big operations to compose existing components, and use smaller operations to build the new parts.
Recall Amdahl's law. Often, the new components are not the cause of the computation bottleneck. Because the performance-critical part is already optimized by the bigger operations, it's okay to forego optimizing the additional small operations, or to do a limited amount of memory optimization instead of operation fusion and directly running them.
Choose Your Own Approach
In this document, we compared multiple approaches to developing programming environments for deep learning. We compared both the usability and efficiency implications of each, finding that many of these trade-offs (like imperative vs symbolic aren't necessarily black and white). You can choose your approach, or combine the approaches to create more interesting and intelligent deep learning libraries.
Contribute to Apache MXNet
This document is part of our effort to provide open-source system design notes for deep learning libraries. If you're interested in contributing to Apache MXNet or its documentation, fork us on GitHub.
